Question

A survey of the TV viewing habits of 50 men and 50 women found the following information: Of the 50 men, 20 prefer watching baseball and 30 prefer football. Of the 50 women, 25 prefer watching baseball and 25 prefer football. Construct a data table for this data and answer the following question: If you randomly select someone who prefers football, what is the probability that the person is a woman?

Answer 1

INFORMATION:

We know that:

- A survey of the TV viewing habits of 50 men and 50 women

- Of the 50 men, 20 prefer watching baseball and 30 prefer football

- Of the 50 women, 25 prefer watching baseball and 25 prefer football

And we must construct a data table for this data and If you randomly select someone who prefers football, find the probability that the person be a woman

STEP BY STEP EXPLANATION:

First, we can organize the information to make the table

- Of the 50 men, 20 prefer watching baseball and 30 prefer football

- Of the 50 women, 25 prefer watching baseball and 25 prefer football

Then, the table that represents the provided data would be

Second, if someone who prefers football is randomly selected and we need to find the probability that this person is a woman, we must divide the number of women that prefers football by the total number of people who prefers football

`\begin{gathered} women\text{ }that\text{ }prefer\text{ }football=25 \\ Total\text{ }of\text{ }people\text{ }who\text{ }prefer\text{ }football=55 \\ (25)/(55)=(5)/(11)=0.4545 \end{gathered}`

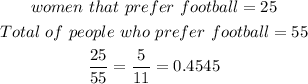
Finally, if someone who prefers football is randomly selected, the probability of being a woman is 0.4545

ANSWER:

Data table:

if someone who prefers football is randomly selected, the probability of being a woman is 5/11 or 0.4545