Answer: Hi! so:
H represent turning left when leaving class and T represent turning right,
Both of them have a 50% probability of happening.
and he wants to know the probability of less than 3 turn left so we wanna know the probability for only one to turn left and the probability for only two.
only one:
if you use the fact that we have a binomial distribution, then the Posibility that only one turns left is:
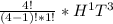
so P(1)= (4!/3!)*
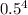 = 4*0.0625 = 0.25
= 4*0.0625 = 0.25
only two:
with the same reasoning.
P(2) = 4!/(2!*2!)*0.0625=6*0.0625 = 0.375
here you can se that the probability is bigger because here are mas combinations that in the previous case.
So the total probability is 0.25 + 0.375 = 0.625.
The fact that he repeats the test n times doesnt change nothing, because he already know that you have a 50/50 chance of turning left of righth