Question

Use the formula for continuous compounding to compute the approximate balance in the account after 1, 5, and 20 years. A $12,000 deposit in an account with an APR of 3.5 percent.

Answer 1

We have that the formula for Continuous Compounding Interest is given by the formula:

`A=P^{}e^(rt)`

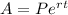
We have from the question, the following information:

1. We need the approximate balance after t = 1, t = 5, t = 20 years.

2. P = $12,000.

3. r = 3.5 ---> r = 3.5/100 = 0.035.

4. e is the value for the e = 2.7172...

Then, we have:

a. Approximated Balance after t = 1. Then, we have:

`A=12000\cdot e^((1\cdot0.035))\Rightarrow A=12427.44`

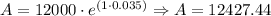
b. Approximated Balance after t = 5. In this case, we can proceed in a similar way:

`A=12000\cdot e^((5\cdot0.035))\Rightarrow A=14294.95`

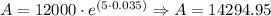
c. Approximated Balance after 20 years:

`A=12000\cdot e^((20\cdot0.035))\Rightarrow A=24165.03`

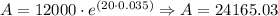
Therefore, the approximated balance in the account after:

One year ---> A = $12427.44.

Five years ---> A = $ 14294.95

Twenty years ---> A = $ 24165.03

By the way, APR is the Annualized Percentage Rate.