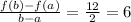Answer:
The average rate of change of the function
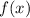 from
from
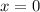 to
to
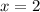 is equal to 6.
is equal to 6.
Explanation:
Let's define the average rate of change of the function
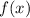 over the interval [a,b] :
over the interval [a,b] :
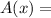 Δf / Δx =
Δf / Δx =
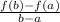
In the exercise,
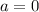 and
and
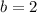
Now we calculate
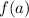 and
and
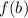
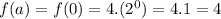
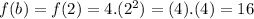
⇒
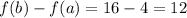 and
and
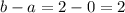
Finally, the average rate of change is