Question

Given g(x) = x² + 1 and g(f(x)) = x² + 4x + 5. Find f .

Answer 1

`f(x)=(x+2)`

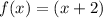
Step-by-step explanation

Step 1

Let

`\begin{gathered} g(x)=x^2+1 \\ g(f(x))=x^2+4x+5 \end{gathered}`

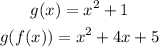
so,

A composite function is generally a function that is written inside another function. Composition of a function is done by substituting one function into another function

so, when evaluate f(x) into g(x) we got

`\begin{gathered} g(x)=x^2+1 \\ g(f(x))=x^2+4x+5 \\ so \\ g(x)=x^2+1 \\ g(f(x))=(f(x))^2+1 \\ \text{hence} \\ (f(x))^2+1=x^2+4x+5 \end{gathered}`

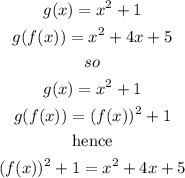
Step 2

solve for f(x)

`\begin{gathered} (f(x))^2+1=x^2+4x+5 \\ \text{subtract 1 in both sides} \\ (f(x))^2+1-1=x^2+4x+5-1 \\ (f(x))^2=x^2+4x+4 \\ \text{factorize} \\ (f(x))^2=(x+2)^2 \\ \text{square root} \\ √((f(x))^2)=√((x+2)^2) \\ f(x)=(x+2) \end{gathered}`

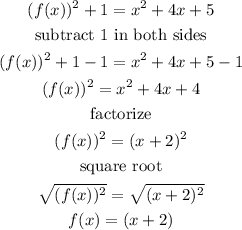
therefore, the answer is

`f(x)=(x+2)`

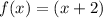
I hope this helps you