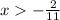Question

Solve the inequality -5/2 (3x-2) < 6-2x. You will need to show and explain every step. You may add more lines if you need them.(I’ve took a picture of the question as well)

Answer 1

Given:

`-(5)/(2)(3x-2)<6-2x`

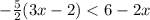
Step 1: Simplify the equation by multiplying -5/2 to the variables inside the parenthesis.

`\begin{gathered} -(5)/(2)(3x-2)<6-2x \\ -(15x)/(2)+5<6-2x \end{gathered}`

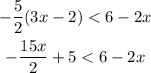
Step 2: Subtract 5 from both sides.

`\begin{gathered} -(15x)/(2)+5<6-2x \\ -(15x)/(2)+5-5<6-2x-5 \\ -(15x)/(2)<1-2x \end{gathered}`

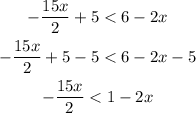
Step 3: Add 2x to both sides.

`\begin{gathered} -(15x)/(2)<1-2x \\ -(15x)/(2)+2x<1-2x+2x \\ -(11x)/(2)<1 \end{gathered}`

Step 4: Multiply both sides by -1 and reverse the inequality.

`\begin{gathered} -(11x)/(2)<1 \\ -(11x)/(2)\cdot(-1)<1\cdot(-1) \\ (11x)/(2)>-1 \end{gathered}`

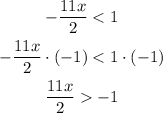
Step 5: Divide both sides by 11/2.

`\begin{gathered} (11x)/(2)>-1 \\ ((11x)/(2))/((11)/(2))>(-1)/((11)/(2)) \\ x>-(2)/(11) \end{gathered}`

ANSWER:

`x>-(2)/(11)`