Question

Which expression is equivalent to (256x^16)^1/4

A.4x^2
B.4x^4
C. 64x^2
D. 64x^4

Answer 1

Answer: The correct option is (B)
`4x^4.`

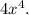
Step-by-step explanation: We are given to select the correct expression that is equivalent to the expression below:

`E=(256x^(16))^(1)/(4).`

We will be using the following properties of exponents:

`(i)~(a^b)^c=a^(b* c),\\\\(ii)~(ab)^c=a^cb^c.`

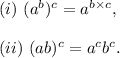
We have

`E\\\\=(256x^(16))^(1)/(4)\\\\=(4^4x^(16))^(1)/(4)\\\\=(4^4)^(1)/(4)(x^(16)^(1)/(4))\\\\=4^{4*(1)/(4)}x^{16*(1)/(4)}\\\\=4x^4.`

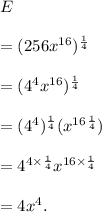
Therefore, the required equivalent expression is
`4x^4.`

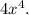
Thus, (B) is the correct option.

Answer 2

Given expression:
`(256x^(16))^(1/4)`.

`\mathrm{Apply\:exponent\:rule}:\quad \left(a\cdot \:b\right)^n=a^nb^n`

`=256^{(1)/(4)}\left(x^(16)\right)^{(1)/(4)}`

`256=4^4`

`256^{(1)/(4)}=\left(4^4\right)^{(1)/(4)}=4`

`\left(x^(16)\right)^{(1)/(4)}=x^{16\cdot (1)/(4)}=x^4`

`(256x^(16))^(1/4) =4x^4`

Therefore, correct option is B option : B.4x^4