Vertical Asymptotes
To answer this question, we can start by finding the vertical asymptotes. For this, we need to set the denominator equal to zero, as follows:
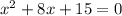
To factor this quadratic equation, we can proceed as follows:
1. We need to find two numbers such as:
a + b = 8
a * b = 15
And these numbers are:
5 + 3 = 8
5*3 = 15
Then, that polynomial can be factored as:
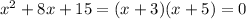
The solutions to this equation are:
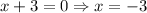
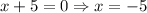
Therefore, these two solutions are the vertical asymptotes of this rational expression (x = -3 and x = -5).
Horizontal Asymptotes
To find them, we need to check the degree of the numerator, n, by looking at the leading term of the polynomial. We also need to check the degree of the denominator, m, of the leading term of the polynomial (written in standard notation).
We can inspect the degree of the numerator:
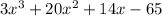
The degree of this polynomial is n = 3.
The degree of the denominator is m = 2:
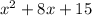
Since we have that the degree of the numerator is greater than the degree of the denominator, that is n > m, we have here that there is no horizontal asymptote:
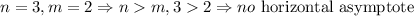
Finding Oblique Asymptotes
To find them, we need to divide the numerator by the denominator. We can do this using the long division process as follows. The resulting quotient will be the equation of the oblique asymptote:
Therefore, the oblique asymptote is a line. The equation is equal to 3x - 4.
Then, the oblique asymptote (slant) is:
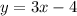
In summary, we have:
Vertical asymptotes:
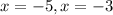
Horizontal asymptotes: None.
Oblique Asymptotes:
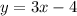
[The answer is the second option:
vertical: x = -5, x = -3.
slant: 3x - 4.]