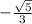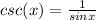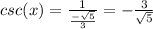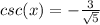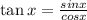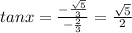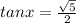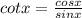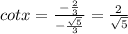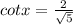Question

Find six trig values if sec(x)=-3/2 and tan(x)>0 I got cos(x)=-2/3 but that is all I could get

Answer 1

I hope this helps you

Answer 2

sin x=
`-(\sqrt5)/(3)`

`csc(x)=-(3)/(\sqrt5)`

`tan x=(\sqrt5)/(2)`

`cot x=(2)/(\sqrt5)`

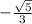
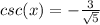
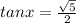
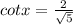
Explanation:

We are given that

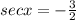`sec x=-(3)/(2)`, cos (x)=
`-(2)/(3)`

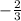
tan x >0

We have to find sinx , csc (x), tan (x), cot (x).

We know that
`sin x=√(1-cos^2x)`

Using the formula

Then, we get

`sin x=\sqrt{1-((-2)/(3))^2}=\sqrt{1-(4)/(9)}=\sqrt{(9-4)/(9)}=(\sqrt5)/(3)`

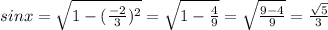
We are given that tan x >0 and cos x(x) <0

It means angle x lies in III quadrant.

In III quadrant , sin x and cos x are both negative and tan x is positive.

Therefore , sin x=
`-(\sqrt5)/(3)`

`csc (x)=(1)/(sinx)`

`csc(x)=(1)/((-\sqrt5)/(3))=-(3)/(\sqrt5)`

`csc(x)=-(3)/(\sqrt5)`

`\tan x=(sinx)/(cosx)`

`tan x=(-(\sqrt5)/(3))/(-(2)/(3))=(\sqrt5)/(2)`

`tan x=(\sqrt5)/(2)`

`cot x=(cos x)/(sinx)`

`cot x=(-(2)/(3))/(-(\sqrt5)/(3))=(2)/(\sqrt5)`

`cot x=(2)/(\sqrt5)`