Question

To the nearest tenth, what is the area of the shaded segment when JA=8ft ??

A. 27.7 ft squared
B. 33.5 ft squared
C. 5.8 ft squared
D. 13.8 ft squared

Answer 1

`A=(1)/(6)\pi 8^2-(8^2√(3))/(4)\approx 5.8\;[ft^2]`
Answer: C. 5.8 ft squared

Answer 2

Answer : The area of the shaded segment is 5.8 ft squared.

Explanation :

Given that,

Length of JA = 8 ft

We have to find the area of the shaded segment. It is given by :

Area of the shaded segment = area of sector - area of the triangle

`A_(seg)=(\theta)/(360)\pi r^2-(1)/(2)r^2sin\theta`

`A_(seg)=(60)/(360)* (22)/(7)* (8)^2-(1)/(2)* (8)^2sin60`

`A_(seg)=5.8\ ft^2`

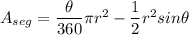
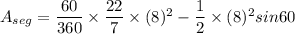
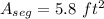
or

`A_(seg)=5.8\ ft\ squared`

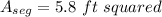
So, the correct option is (C) " 5.8 ft squared".