Question

Prove that the limit x tends to 1 (2x^4-6x^3+x^2+3)÷(x-1)=-8

Answer 1

First note that if
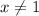
`x\\eq1`, you have


`(2x^4-6x^3+x^2+3)/(x-1)=2x^3-4x^2-3x-3`

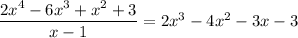
Now, you're looking for
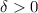
`\delta>0` such that for any
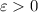
`\varepsilon>0`, you have


`|x-1|<\delta\implies|2x^3-4x^2-3x-3+8|=|2x^3-4x^2-3x+5|<\varepsilon`

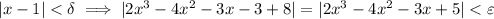
Note that you can divide through the left side of the
`\varepsilon` inequality by
`x-1` once more:


`(2x^3-4x^2-3x+5)/(x-1)=2x^3-2x-5\implies 2x^3-4x^2-3x+5=(x-1)(2x^2-2x-5)`

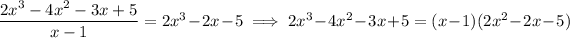
So it follows that you need to find an appropriate
`\delta` that will guarantee


`|(x-1)(2x^2-2x-5)|=|x-1||2x^2-2-5|<\varepsilon`

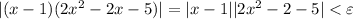
For the moment, let's fix
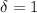
`\delta=1`. Then by this assumption, we have


`|x-1|<\delta=1\implies-1<x-1<1\implies0<x<2`

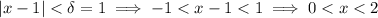
From this we get


`\implies0<x^2<4`

`\implies0<x^2-x<4-2\implies 0<x^2-x<2`

`\implies0<2x^2-2x<4`

`\implies-5<2x^2-2x-5<-1`

`\implies1<|2x^2-2x-5|<5`

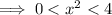
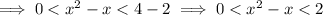
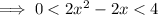
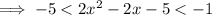
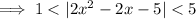
where the upper bound is what we care about. With this assumption, we then get that


`|x-1||2x^2-2-5|<5|x-1|<\varepsilon\implies|x-1|<\frac{\varepsilon}5`

which suggests that
`\delta` can be taken to be either the smaller of 1 or
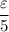
`\frac{\varepsilon}5`, or
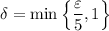
`\delta=\min\left\{\frac{\varepsilon}5,1\right\}`, to guarantee that the function gets arbitrarily close to -8.