Answer:
 or 1 to 7.
or 1 to 7.
Explanation:
We are asked to find the odds against rolling a 6 on a eight-sided die.
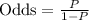 , where p represents probability of an event.
, where p represents probability of an event.
We will find probability of getting 6 on an 8 sided die as:
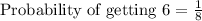
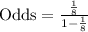
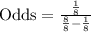
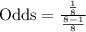
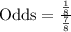
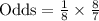
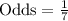
Therefore, the odds against rolling a 6 is 1 to 7.