Solution
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given combination expression
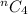
STEP 2:Write the formula for combination

STEP 3: Substitute the values

Rewrite n!
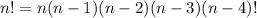
We stop at (n-4)! so that it can be used to cancel out the (n-4)! which is the denominator of the combination expression. Therefore, we have:
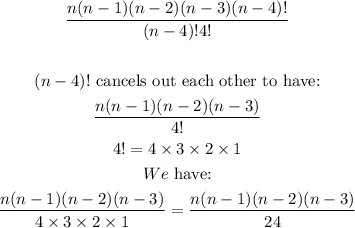
Hence, the reason for having the expression in the image question.