Question

Why does it's stops at (n-3)? shouldn't it continue until (n-x)=1?

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given combination expression

`^nC_4`

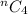
STEP 2:Write the formula for combination

`^nC_r=(n!)/((n-r)!r!)`

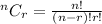
STEP 3: Substitute the values

`^nC_4=(n!)/((n-4)!4!)`

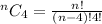
Rewrite n!

`n!=n(n-1)(n-2)(n-3)(n-4)!`

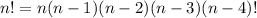
We stop at (n-4)! so that it can be used to cancel out the (n-4)! which is the denominator of the combination expression. Therefore, we have:

`\begin{gathered} (n(n-1)(n-2)(n-3)(n-4)!)/((n-4)!4!) \\ \\ (n-4)!\text{ cancels out each other to have:} \\ (n(n-1)(n-2)(n-3))/(4!) \\ 4!=4*3*2*1 \\ We\text{ have:} \\ (n(n-1)(n-2)(n-3))/(4*3*2*1)=(n(n-1)(n-2)(n-3))/(24) \end{gathered}`

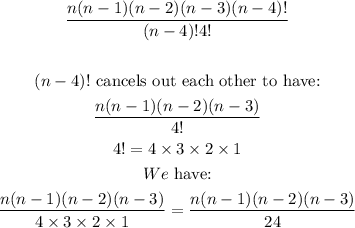
Hence, the reason for having the expression in the image question.