Question

A cylinder and a cone have congruent heights and radii.what is the ratio of the volume of the cone to the volume of the cylinder?

Answer 1

cone=(hpr^2)/3, cylinder=hpr^2, so the ratio:

cone:cylinder=1/3:1 or using integers by convention:

cone:cylinder=1:3

Answer 2

1: 3 ratio of the volume of the cone to the volume of the cylinder

Explanation:

Volume of cone(V) is given by:

`V = (1)/(3) \pi r^2h`

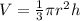
where, r is the radius and h is the height of the cone.

Volume of cylinder(V') is given by:

`V' = \pi r'^2h'`

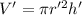
where, r' is the radius and h' is the height of the cylinder.

As per the statement:

A cylinder and a cone have congruent heights and radii.

⇒r = r' and h = h'

then;

`(V)/(V') = ( (1)/(3) \pi r^2h)/(\pi r'^2h') = ( (1)/(3) \pi r'^2h')/(\pi r'^2h')`

⇒
`(V)/(V') =(1)/(3) = 1 : 3`

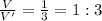
Therefore, the ratio of the volume of the cone to the volume of the cylinder is, 1 : 3