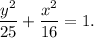Answer: The required equation of the ellipse in standard form is
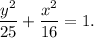
Step-by-step explanation: We are given to find the equation of an ellipse in standard form with the vertical major axis of length 10 units and minor axis of length 8 units.
Since the major axis is vertical, so it will lie on the Y-axis. Let the standard form of the ellipse be given by

where the length of major axis is 2a units and length of minor axis is 2b units.
According to the given information, we have

and
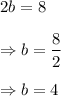
Substituting the values of a and b in equation (i), we get
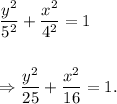
Thus, the required equation of the ellipse in standard form is