The formula for the volume of a pyramid is:
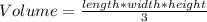
Let's pretend that we have a pyramid with a length of 3 and a width of 3 and a height of 6. If we plug this into the formula, we get
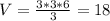
Now, let's pretend the height is 3.
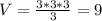
9 is half of 18. This works for any numbers you plug in. If you half the height, than the volume is also halved.