Explanation :
(a) Initial velocity, v₁ = 60 mph
Final velocity, v₂ = 20 mph
Let KE₁ and KE₂ are the initial and final kinetic energies.
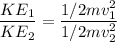
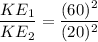
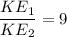
So, the kinetic energy increases 9 times.
(b) Initial velocity, v₁ = 60 mph
Final velocity, v₂ = 30 mph
Let KE₁ and KE₂ are the initial and final kinetic energies.
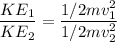
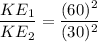
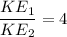
So, the kinetic energy increases 4 times.
Hence, this is the required solution.