Question

An object has a constant acceleration of 40 ft/sec2, an initial velocity of −20 ft/sec, and an initial position of 10 ft. Find the position function, s(t), describing the motion of the object.

I'm all the way up to here, what do I do now?
a(t)=40 v(0)=-20 s(0)=10
the integral of 40 dt, antiderivative is v(t)=40t+C
40(0)+C=-20
C=-60
s(t)=integral of (40(t)-60)dt
antiderivative is 20t^2-60t+C

Answer 1

d2x/dt2=40

dx/dt=40t+vo and vo=-20 so

dx/dt=40t-20

x(t)=40t^2/2-20t+x0 and x0=10 so

x(t)=20t^2-20t+10

Answer 2

The equation that describes the motion of the object is
`s(t)=20t^2-20t+10`

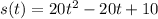
Explanation:

It is given that,

Acceleration of the object at time t is:

`a(t)=40\ ft/s^2`

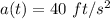
Initial velocity or velocity at t = 0,
`v(0)=-20\ ft/s`

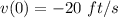
Initial position or position at t = 0,
`s(0)=10\ ft`

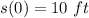
Since,
`v(t)=\int\limits {a(t).dt}`

`v(t)=\int\limits {40.dt}`

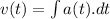
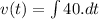
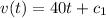`v(t)=40t+c_1`............(1)

At t = 0,
`v(0)=-20\ ft/s`

→
`c_1=-20`

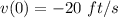
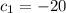
Equation (1) becomes :

`v(t)=40t-20`

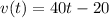
Since,
`s(t)=\int\limits {v(t).dt}`

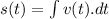
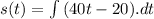
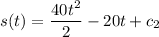`s(t)=\int\limits {(40t-20).dt}`

`s(t)=(40t^2)/(2)-20t+c_2`............(2)

At t = 0,
`s(0)=10\ ft/s`

→
`c_1=10`

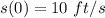
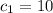
Equation (2) becomes:

`s(t)=20t^2-20t+10`

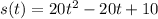
Hence, this is the required solution.