Answer:
Explanation:
As given that ,
tan(Ф)=3/4
Now to find sect(Ф)
we know that,
1+
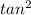 (Ф)=
(Ф)=
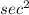 (Ф)
(Ф)
putt values we get ,
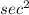 (Ф)=1+(3/4)^2
(Ф)=1+(3/4)^2
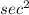 (Ф)=1+9/16
(Ф)=1+9/16
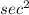 (Ф)=25/16
(Ф)=25/16
sec(Ф)= +5/4 and sec(Ф)=-5/4 as quadrant is not mentioned so will take both positive and negative values
hence we get ,
tan(Ф)+sec(Ф)=3/4+5/4 = 8/4 = 2
also for sec(Ф)= -5/4
tan(Ф)+sec(Ф)= 3/4-5/4 = -2/4 = -1/2