For a > b > c 0 and a + b + c = 1, show that a^(2) + 3b^(2) + 5c^(2) \ \textless \ 1

Question

For a > b > c 0 and a + b + c = 1,

show that
`a^(2) + 3b^(2) + 5c^(2) \ \textless \ 1`

Answer 1

Starting with what we know:

`a + b + c = 1` is the same as:

`(a + b + c)^(2) = 1^(2)`

`a^(2) + b^(2) + c^(2) + 2(ab + bc + ac) = 1`

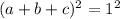
Now, let's use our inequality and bring it into our equation.
Since a > b and b >0, then a > 0
Thus, we can multiply both sides by a, b, or c since they are all positive values.

We can say:
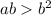
`ab > b^(2)`, since b > 0
Similarly,
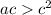
`ac > c^(2)` and
`bc > c^(2)`

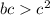
Now, we've got values for ab, ac, and bc.
Using this information back into our original equation:

`a^(2) + b^(2) + c^(2) + 2(ab + bc + ac) = 1`

Since
`ab > c^(2)`, then we can say:

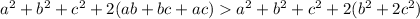
`a^(2) + b^(2) + c^(2) + 2(ab + bc + ac) > a^(2) + b^(2) + c^(2) + 2(b^(2) + 2c^(2))` and

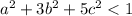
`a^(2) + 3b^(2) + 5c^(2) < 1` as required.