Question

For accounting purposes, the value of assets (land, buildings, equipment) in a business are depreciated at a set rate per year. The value, V(t), of $775,000 worth of assets after t years, that depreciate at 15% per year, is given by the formula V(t) = V0(b)t. What is the value of Vo and b, and when rounded to the nearest cent, what are the assets valued at after 6 years?

Vo = $775,000, b = 0.85, and the value after 6 years is $289,324.17
Vo = $775,000, b = 0.15, and the value after 6 years is $8.82
Vo = $775,000, b = 1.15, and the value after 6 years is $697,500.00
Vo = $775,000, b = 0.85, and the value after 6 years is $292,290.87

Answer 1

Vo= $775,000, b = 0.85, and the value after 6 years is $292,290.87

Answer 2

Vo = $775,000, b = 0.85, and the value after 6 years is $292,290.87

Explanation:

The formula
`V(t)=Vo(b)^(t)`

Vo is the value of assets = $775000

b = 1-r

r = rate of depreciation = 15% or 0.15

b =1−0.15=0.85

T= time ( number of years ) = 6

So after 6 years the value of the assets will be :

V(6)=
`775000*(0.85)^(6)`

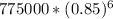
= 775000*0.37714 = $292283.50

This is closest to $292,290.87, therefore, option D is the answer.

Vo = $775,000, b = 0.85, and the value after 6 years is $292,290.87