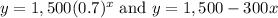Answer:
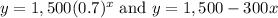
Explanation:
Given : Ron buys a lawnmower for $1,500. The salesperson says the value will depreciate about 30% per year (r=0.3) over the next few years.
The exponential decay equation is given by :-
 , where A is the initial amount , r is rate of decay and x is the time period.
, where A is the initial amount , r is rate of decay and x is the time period.
Then , the equation of depreciation for Ron :-
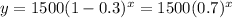
However, his neighbor says it is likely to depreciate about $300 per year, which is linear depreciation.
The linear equation is given by :-
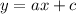 , where 'c' is the initial amount and 'a' is the rate of change.
, where 'c' is the initial amount and 'a' is the rate of change.
Then equation of depreciation for his neighbor :-
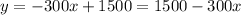
Thus , the system could be used to determine when the two depreciation models will give the same value for the lawnmower:-