Note that
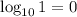
,
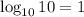
,

, and so on. The function
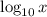
is continuous and increasing for all
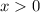
, so when
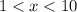
, we have
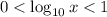
; when
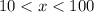
,
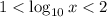
; and so on.
This means

which means we can capture the number of digits of
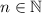
with the function
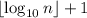
.
So the problem is the same as finding positive integer solutions to
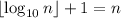
We know that
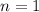
has one digit, so clearly this must be a solution. We need to show that this is the only solution.
Recall that
![(\mathrm d)/(\mathrm dx)[\log_(10)x+1]=\frac1{\ln10\,x}](https://img.qammunity.org/2018/formulas/mathematics/college/5vysn8tejdyxobnifo5hz476f3on3bcwxm.png)
, while
![(\mathrm d)/(\mathrm dx)[x]=1](https://img.qammunity.org/2018/formulas/mathematics/college/l6qzybt8qashhvle365ma35424nejswywp.png)
. This means
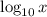
increases at a much slower rate than

as
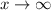
. We know the two functions intersect when
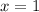
. Therefore it's clear that
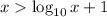
for all
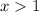
.
Now, it's always the case that

, so we're essentially done:
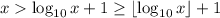
which means there are no other solutions than
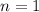
.