You've established that
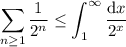
so all you need to do is compute the integral. Rewrite the integrand as

and replace
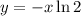
, so that
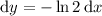
. Then
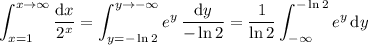
By the fundamental theorem of calculus, this evaluates to

and so the series converges.
You also could have used the fact that the series is geometric with common ratio less than 1 to arrive at the same conclusion, with the added perk of being able to find the exact value of the sum to corroborate this.