Recall that the secant function is the reciprocal function to the cosine function.
Also, recall that sin²x + cos²x = 1 and 1 - sin²x = cos²x
Thus, we can rewrite the equation as:
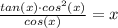
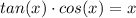
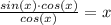
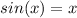
There's only one point at which sin(x) = x, and that's at x = 0.
Thus, x = 0 is the only solution.