Question

Is this a recursive pattern, a geometric sequence or a arithmetic sequence? Can it be solved? 6, 24, 26, 28,32,...

Answer 1

Given the sequence:

`6,24,26,28,32,...`

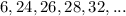
You need to remember that:

- In a Geometric Sequence, each term is found by multiplying the previous term by a constant called "Common ratio".

- In an Arithmetic Sequence, the difference between a term and its previous term is constant.

In this case, you can check if it is a Geometric Sequence by dividing the terms by the corresponding previous term:

`\begin{gathered} (24)/(6)=4 \\ \\ (26)/(24)\\e4 \end{gathered}`

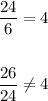
It is not a Geometric Sequence, because it does not have a Common Ratio.

To check it if is an Arithmetic Sequence, find the difference between the terms:

`\begin{gathered} 24-6=18 \\ 26-24=2 \end{gathered}`

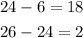
As you can see, it is not an Arithmetic Sequence, because the difference between the terms is not constant.

Then, the sequence is neither geometric nor arithmetic.

Knowing this, you need to find a Recursive Formula for the sequence. You can identify that:

`\begin{gathered} a_2=6\cdot4=24 \\ a_3=a_2+2 \\ a_4=a_3+2 \\ a_5=a_4+4 \end{gathered}`

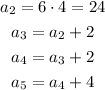
However, as you can notice, there is not a defined pattern between the terms shown in the exercise. Therefore, it cannot be solved.

Therefore, you can determine that the answer is: It is a Recursive Pattern. It cannot be solved.