Before we graph the given equation, let's convert it to slope-intercept form first. Here are the steps.
1. Subtract 5 on both sides of the equation.
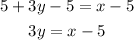
2. Next, divide both sides of the equation by 3.
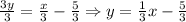
We have converted the equation to slope-intercept form.
The slope is 1/3 and the y-intercept is -5/3 or -1.67.
To complete the given coordinate, simply replace "x" with the given x-coordinate and solve for y in the slope-intercept form.
Let's start with (2, ?) which is x = 2.
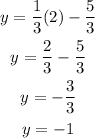
At x = 2, y = -1. Completing the first coordinate, we have (2, -1).
Next, at x = -1.
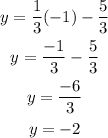
Completing the second coordinate, we have (-1, -2).
Lastly, at x = -4:
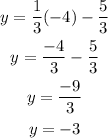
Completing the third coordinate, we have (-4, -3).
The graph of this equation is shown below: