Question

I am supposed to use the slope-intercept method to graph this equation5 + 3y = xComplete the coordinates: (2, ?) - (-1, ?) - (-4, ?)

Answer 1

Before we graph the given equation, let's convert it to slope-intercept form first. Here are the steps.

1. Subtract 5 on both sides of the equation.

`\begin{gathered} 5+3y-5=x-5 \\ 3y=x-5 \end{gathered}`

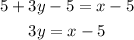
2. Next, divide both sides of the equation by 3.

`(3y)/(3)=(x)/(3)-(5)/(3)\Rightarrow y=(1)/(3)x-(5)/(3)`

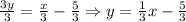
We have converted the equation to slope-intercept form.

The slope is 1/3 and the y-intercept is -5/3 or -1.67.

To complete the given coordinate, simply replace "x" with the given x-coordinate and solve for y in the slope-intercept form.

Let's start with (2, ?) which is x = 2.

`\begin{gathered} y=(1)/(3)(2)-(5)/(3) \\ y=(2)/(3)-(5)/(3) \\ y=-(3)/(3) \\ y=-1 \end{gathered}`

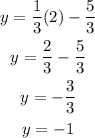
At x = 2, y = -1. Completing the first coordinate, we have (2, -1).

Next, at x = -1.

`\begin{gathered} y=(1)/(3)(-1)-(5)/(3) \\ y=(-1)/(3)-(5)/(3) \\ y=(-6)/(3) \\ y=-2 \end{gathered}`

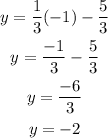
Completing the second coordinate, we have (-1, -2).

Lastly, at x = -4:

`\begin{gathered} y=(1)/(3)(-4)-(5)/(3) \\ y=(-4)/(3)-(5)/(3) \\ y=(-9)/(3) \\ y=-3 \end{gathered}`

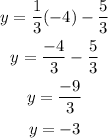
Completing the third coordinate, we have (-4, -3).

The graph of this equation is shown below: