Answer:
$3712.
Explanation:
We have been given that Aileen deposited money into an account compounded semiannually at a rate of 2.1%.
To find the principal amount we will use compound interest formula.
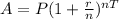 , where,
, where,
A= Amount after T years,
P =Principal amount,
r = Interest rate in decimal form,
n = Number of times interest is compounded per year,
T = Time in years.
Let us convert our given interest rate in decimal form.
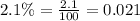
Upon substituting our given values in above formula we will get,
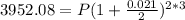
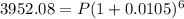
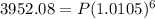
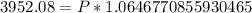
Let us divide both sides of our equation by 1.0646770855930465.
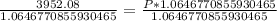
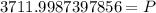
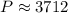
Therefore, Aileen deposited approximately $3712 in her account.