ANS: power of a quotient property
(x/y)^n = x^n / y ^n ( power of quotient )
x^m/x^n = x^(m-n) (Quotient of power)
x^m x^n = x^(m+n) (Product of powers) < Same base >
x^(m^n) (Power of Power)
In your case you have (2/5)^3 -> 2/5 is called a quotient ( fraction ) when you raise it to power ( ^3) it's power of quotient
Power = multiple repetitions of multiplication
(2/5)^3 = 2/5 multiplied by itself 3 times = 2/5 * 2/5 * 2/5
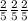
in multiplication you simply multiply all terms in the denominator times each other and all terms in the nominator times each other
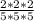
we know that repetitive multiplication = power , we have 3 terms in the denominator 2 2 2
so = 2^3 ( 3 because it's repeated 3 times )
same for the denominator we get 5^3

2^3 = 2 x 2 x 2 = 8
5^3 = 5 x 5 x 5 = 125
= 8/125
Proving such property in general requires the use of Proof by induction in which you have 3 basic steps < basic step (proof for 1 or 0) , assume true for n , proof for n + 1 or simple induction start from 0 repeat until you have a pattern and induce the general formula)
x/y * x/y = x^2/y^2 = (x/y)^2
x/y * x/y * x/y = x^3/y^3 = (x/y)^3
......
x/y * x/y * x/y * ...... n = (x/y)^n