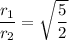Answer:
The simplified radical form is given as:
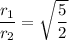
Explanation:
It is given that:
the ratio of the diffusion rates of two gases is given by the formula:
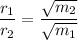
where
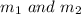 are the masses of the molecules of the two gases.
are the masses of the molecules of the two gases.
Now we are given:
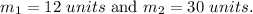
Hence,
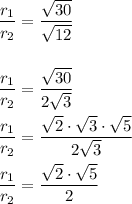
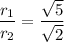
Hence, the simplified radical form is: