Question

Binomial Theorem The constant term in the expansions of (px^3 + q/x ^3)^8 and (px^2 + q/x^2)^4are equal, and p and q are both greater than zero. Express p in terms of q.

Answer 1

Given the expressions :

`\begin{gathered} (px^3+(q)/(x^3))^8 \\ \\ (px^2+(q)/(x^2))^4 \end{gathered}`

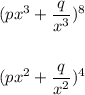
The constant term in the expansions are equal

So, the constant term of the first expansion is :

`^nC_r\cdot(px^3)^(n-r)\cdot((p)/(x^3))^r`

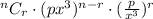
The constant term will appear when :

`\begin{gathered} n-r=r \\ n=2r \\ r=(n)/(2)=(8)/(2)=4 \end{gathered}`

So, the constant term is :

`^8C_4\cdot(px^3)^4\cdot((p)/(x^3))^4=70\cdot p^4\cdot q^4`

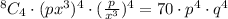
And for the second expansions : n = 4

so, the constant term is :

`^4C_2\cdot(px^2)^2\cdot((q)/(x^2))^2=6\cdot p^2\cdot q^2`

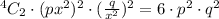
So, the constants are equal :

`70\cdot p^4\cdot q^4=6\cdot p^2\cdot q^2`

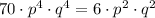
Divide both sides by (p^2 * q^2 )

`\begin{gathered} (70p^4q^4)/(p^2q^2)=(6p^2q^2)/(p^2q^2) \\ \\ 70p^2q^2=6 \end{gathered}`

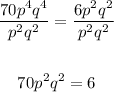
Solve for p :

`\begin{gathered} p^2=(6)/(70q^2) \\ \\ p=\sqrt[]{(6)/(70)}\cdot(1)/(q) \end{gathered}`

We can write q in terms of p as following :

`q=\sqrt[]{(6)/(70)}\cdot(1)/(p)`