Question

please help me go through this question, I got it wrong, and the correct answer is in the gray box, I just want to know what process I was supposed to go through to get that answer. thank you!

Answer 1

Lighthouse B is 8 miles from lighthouse A,

The diagram below shows the representation of the details of the question

Let x represents the distance of the boat from B

To find x, we use the cosine rule which is

`b^2=a^2+c^2-2ac\cos B_{}_{}`

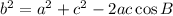
Where

`\begin{gathered} a=x \\ b=6 \\ c=8 \\ B=25\degree \end{gathered}`

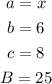
Substitute the values into the formula above

`\begin{gathered} 6^2=x^2+8^2-2(x)(8)\cos 25\degree \\ 36=x^2+64-16x\cos 25\degree \\ x^2+64-36-16x\cos 25\degree=0 \\ x^2+28-14.5x=0 \\ x^2-14.5x+28=0 \end{gathered}`

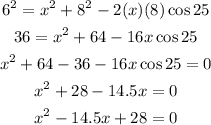
Solving for x, using the quadratic formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where

`a=1,b=-14.5,c=28`

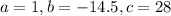
Substitute the values of a, b and c into the formula above

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-14.5)\pm\sqrt[]{(-14,5)^2-4(1)(28)}_{}}{2(1)} \\ x=\frac{14.5\pm\sqrt[]{210.25-112}}{2} \\ x=\frac{14.5\pm\sqrt[]{98.25}}{2} \end{gathered}`

The values of x will be

`\begin{gathered} x=\frac{14.5\pm\sqrt[]{98.25}}{2} \\ x=(14.5\pm9.9121)/(2) \\ x=(14+9.9121)/(2)=12.2\text{ (nearest tenth)} \\ x=(14-9.9121)/(2)=2.3\text{ (nearest tenth)} \end{gathered}`

The values of x are

`x=12.2\text{ or 2.3}`

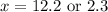
Hence, the boat is either 12.2 miles or 2.3 miles (nearest tenth) from lighthouse B.