Solution
Lighthouse B is 8 miles from lighthouse A,
The diagram below shows the representation of the details of the question
Let x represents the distance of the boat from B
To find x, we use the cosine rule which is
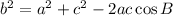
Where

Substitute the values into the formula above
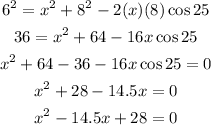
Solving for x, using the quadratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
Where
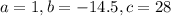
Substitute the values of a, b and c into the formula above
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-14.5)\pm\sqrt[]{(-14,5)^2-4(1)(28)}_{}}{2(1)} \\ x=\frac{14.5\pm\sqrt[]{210.25-112}}{2} \\ x=\frac{14.5\pm\sqrt[]{98.25}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ntsrw6a37z1ie97g03c2.png)
The values of x will be
![\begin{gathered} x=\frac{14.5\pm\sqrt[]{98.25}}{2} \\ x=(14.5\pm9.9121)/(2) \\ x=(14+9.9121)/(2)=12.2\text{ (nearest tenth)} \\ x=(14-9.9121)/(2)=2.3\text{ (nearest tenth)} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/klabm2mciesnblx1hri1.png)
The values of x are
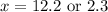
Hence, the boat is either 12.2 miles or 2.3 miles (nearest tenth) from lighthouse B.