Question

In how many distinct ways can the letters of the word atlanta be arranged?

Answer 1

There are 7! ways in arranging 7 objects into 7 spaces. But we've overcounted by a factor of 3! (a's can interchange in 3! ways), and 2! (t's can interchange in 2! ways).

To better understand this concept, let's name each repeated letter:
a₁ t₁ l a₂ n t₂ a₃

Now, we can rearrange atlanta to make:
a₂ t₂ l a₃ n t₁ a₁

Without the superscripts, we make atlanta. But wait... we've already made that word with:
a₁ t₁ l a₂ n t₂ a₃

This is because we need to account for the times the a's can change and we wouldn't notice, and the t's can change and we won't notice.

Thus, our final number of ways becomes:

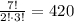
`(7!)/(2! \cdot 3!) = 420` different ways.