Question

OAB is a triangle

M is the midpoint of OA
N is the midpoint of OB
Show that AB is parallel to MN

Answer 1

Construct MN.
Since M is the midpoint of OA, OM = MA
Similarly, N is the midpoint of OB.
Thus, ON = NB.

Now, in Δs OMN and OAB,
∠MON = ∠AOB (common angle)

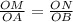
`(OM)/(OA) = (ON)/(OB)` (sides are in proportional ratio; OA = 2OM and OB = 2ON)

∴ Δs OMN and OAB are similar (2 sides are in proportion, with the included angle)
Since they are similar, then ∠OMN = ∠OAB (corresponding angles of similar triangles are equal)
But since ∠OMN = ∠OAB, then that means MN || AB (corresponding angles of two lines must be equal since they also sit relative to the transverse line, OA)

Thus, AB || MN (QED)