Question

EXPLAIN why we placed the value of x= 4/3( the minimum value) into the equ of gradient(dy/dx) [in the answer, marking scheme attached] to get the answer -4/3 ?? Isn't 4/3 the minimum value???

Answer 1

`y=x(x-2)^2`

`\implies y'=(x-2)^2+2x(x-2)=3x^2-8x+4=(3x-2)(x-2)=0`

`\implies x=\frac23,x=2`

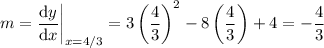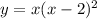
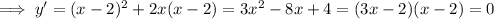
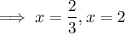
are the critical points, and judging by the picture alone, you must have
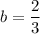
`b=\frac23` and
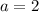
`a=2`. (You might want to verify with the derivative test in case that's expected.)

Then the shaded region has area


`\displaystyle\int_0^2x(x-2)^2\,\mathrm dx=\frac43`

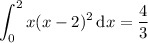
I'll leave the details to you.

Now, for part (iv), you're asked to find the minimum of
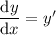
`(\mathrm dy)/(\mathrm dx)=y'`, which entails first finding the second derivative:


`y'=3x^2-8x+4`

`\implies y''=6x-8`

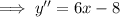
setting equal to 0 and finding the critical point:


`6x-8=0\implies x=\frac86=\frac43`

This is to say the minimum value of
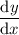
`(\mathrm dy)/(\mathrm dx)` *occurs when
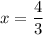
`x=\frac43`*, but this is not necessarily the same as saying that
`\frac43` is the actual minimum value.

The minimum value of
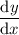
`(\mathrm dy)/(\mathrm dx)` is obtained by evaluating the derivative at this critical point:


`m=(\mathrm dy)/(\mathrm dx)\bigg|_(x=4/3)=3\left(\frac43\right)^2-8\left(\frac43\right)+4=-\frac43`