Question

In the hyperbola, 4x^2 − 9y^2 = 36, the focci are located at:a. (±6,0)b. (0,±6c. (±√13, 0)d. (0, ±√13)e. (0,0)

Answer 1

Since the equation of the hyperbola is

`4x^2-9y^2=36`

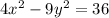
Divide all terms by 36

`\begin{gathered} (4x^2)/(36)-(9y^2)/(36)=(36)/(36) \\ (x^2)/(9)-(y^2)/(4)=1 \end{gathered}`

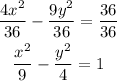
Since the form of the equation of the hyperbola is

`(x^2)/(a^2)-(y^2)/(b^2)=1`

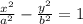
By comparing them

`\begin{gathered} a^2=9 \\ b^2=4 \end{gathered}`

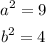
Since the foci are (c, 0) and (-c, 0)

Since the value of c can be found from the rule

`c^2=a^2+b^2`

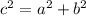
Then

`\begin{gathered} c^2=9+4 \\ c^2=13 \end{gathered}`

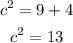
Find the square root of both sides

`c=\pm\sqrt[]{13}`

The foci are

`(\sqrt[]{13},0),(-\sqrt[]{13},0)`

Then the answer is C