Since the equation of the hyperbola is
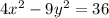
Divide all terms by 36
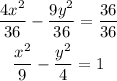
Since the form of the equation of the hyperbola is
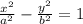
By comparing them
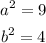
Since the foci are (c, 0) and (-c, 0)
Since the value of c can be found from the rule
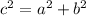
Then
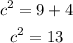
Find the square root of both sides
![c=\pm\sqrt[]{13}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/vfrd27z2ucu477z1t0v4.png)
The foci are
![(\sqrt[]{13},0),(-\sqrt[]{13},0)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/w6ebh5hv3s00oaslrbuo.png)
Then the answer is C