Question

How many distinguishable 11 letter​ "words" can be formed using the letters in MISSISSIPPI​?

Answer 1

This is given by the multinomial coefficient:


`\dbinom{11}{1,4,4,2}=(11!)/(1!4!4!2!)=34650`

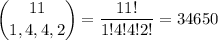
If you're not familiar with the multinomial coefficient, you may be able to see it more clearly if you count the number of possible combinations taking each distinct letter
`n` times, where
`n` is the number of times it shows up in the original word.


`\underbrace{\dbinom{11}1}_{\text{M}}\underbrace{\dbinom{10}4}_{\text{I}}\underbrace{\dbinom64}_{\text{S}}\underbrace{\dbinom22}_{\text{P}}=(11!)/(1!10!)(10!)/(4!6!)(6!)/(4!2!)(2!)/(2!0!)=(11!)/(1!4!4!2!)`