Question

Write y=2x^2+8x+10 in vertex form?

Answer 1

`\bf y=2x^2+8x+10\impliedby \textit{let's start by grouping} \\\\\\ y=(2x^2+8x)+10\implies y=2(x^2+4x+\boxed{?}^2)+10`

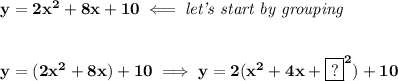
hmmm we seem to be missing a value there, to get a "perfect square trinomial" from the group... what can that be?
hmm, well, recall, the middle term of a perfect trinomial, is 2 * [guy on the left] * [guy on the right]

now, the middle term, would be 4x, so, we know that 2 * x * [?] = 4x
well
`\bf 2\cdot x\cdot \boxed{?}=4x\implies \boxed{?}=\cfrac{4x}{2x}\implies \boxed{?}=2`

so, that's our missing fellow, is 2, now, keep in mind, all we're doing is borrowing from our very good friend Mr Zero, 0, so, if we add 2², we have to also subtract 2²

thus
`\bf y=2(x^2+4x+2^2-2^2)+10\\\\\\ y=2(x^2+4x+2^2)-2^2\cdot 2+10 \\\\\\ y=2(x+2)^2-8+10\implies y=2(x+2)^2+2`

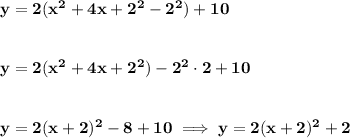
notice, the -2 was inside, with a common factor of 2, so it was really 2*-2², or -8 when it came out of the group

anyhow, that's the so-called "completing the square", and that's the vertex form of the parabola, whose vertex is clearly at -2, 2

Answer 2

the answer is -2 you use the formula -b over 2a