Answer:
Therefore, the new pressure is 417.455 kPa
Explanation:
As per general gas equation
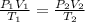
If Volume of a gas is constant then equation is represented by
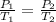
Here
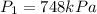 and
and
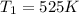
If
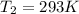 then we have to calculate the value of
then we have to calculate the value of
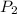
Now we plug in the values in the equation
\frac{748}{525}=\frac{P_{2}}{293}
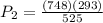
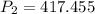 kPa
kPa
Therefore, the new pressure is 417.455 kPa