Question

The cost, in dollars, to produce vats of ice cream is C(x) = 2x+4. When selling them to ice creamshops, the price-demand function, in dollars per vat, is p(x) = 116 - 32Find the profit function.P(x)How many vats of ice cream need to be sold to maximize the profit.vats of ice creamFind the maximum profit.dollars

Answer 1

From the question,

The cost is given by the function

`C(x)=2x+4`

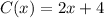
And the price demand function is given by the function

`p(x)=116-3x`

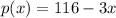
Now profit is calculated as

`P(x)=xp(x)-C(x)`

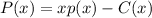
So we have

`\begin{gathered} P(x)=xp(x)-C(x) \\ P(x)=x(116-3x)-(2x+4) \\ =116x-3x^2-2x-4 \\ =-3x^2-114x-4 \end{gathered}`

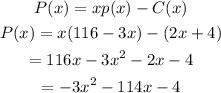
Hence the profit function is

`P(x)=-3x^2-114x-4`

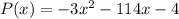
At maximum profit, the derivative of the function for profit is equal to zero, we have

`\begin{gathered} P(x)=-3x^2-114x-4 \\ P^(\prime)(x)=-6x^{}-114 \\ -6x^{}-114=0 \\ 6x=-114 \\ x=(-114)/(6) \\ x=-19 \end{gathered}`

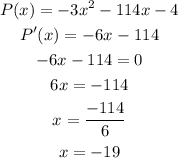
So we can see that the answer to that is -19

The maximum profit becomes ,

we substitute x for -19, we have

`\begin{gathered} P(-19)=-3x^2-114x-4 \\ P(-19)=-3(-19)^2-114(-19)-4 \\ =-1,083+2,166-4 \\ =1,079 \end{gathered}`

Hence the maximum profit is $1,079