Question

Point O is the incenter of ΔABC.

What is mQBO?

mQBO is ___ degrees.

Answer 1

the answer is 12 degrees

Answer 2

`m\angle QBO=12`

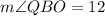
Explanation:

We have been given that point O is the in-center of triangle ABC. We are asked to find the measure of angle QBO.

We know that in-center of a triangle is the point, where three angle bisectors of triangle meet.

Since O is in-center, so AO will be angle bisector. We will find the value of x by equating the expression for angle QAO to angle SAO as:

`2x+6=4x-12`

`2x+6-6=4x-12-6`

`2x=4x-18`

`2x-4x=4x-4x-18`

`-2x=-18`

`(-2x)/(-2)=(-18)/(-2)`

`x=9`

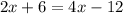
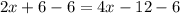
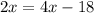
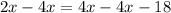
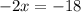
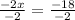
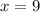
Now we will substitute
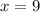`x=9` in the expression for measure of angle QBO.

`m\angle QBO=3x-15`

`m\angle QBO=3*9-15`

`m\angle QBO=27-15`

`m\angle QBO=12`

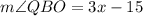
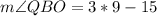
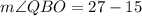
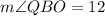
Therefore, the measure of angle QBO is 12 degrees.