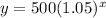Answer:
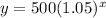
Explanation:
Given: The value of a collector’s item is expected to increase exponentially each year.
The exponential growth equation is given by :
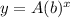 , where A is the initial cost , b is the growth factor per year and x is the number of years.
, where A is the initial cost , b is the growth factor per year and x is the number of years.
The cost of item A= $500
After 2 years, the item is worth $551.25 (y), then we have the following equation
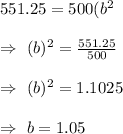
When we substitute the values of A and b in the standard equation, we get equation represents y, the value of the item after x years will be: