Answer:
Two points that satisfy the system propose are P1 = (3, 1) and P2 = (0, 4).
Explanation:
Despite this equation system could be solve in different ways, as many things in Math do, we can take advantage of the negative symbol of equation y = -x^{2}+ 2x + 4. Yes, instead of solving this using the quadratic formula, and doing so many other steps, and with the high probability of making a mistake observing that
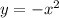 , we can solve this system using the well known logical formula that if x = b and y = b, then x = y.
, we can solve this system using the well known logical formula that if x = b and y = b, then x = y.
First Step: the way of solving this system
This equation system could be solve in the following way:
First, we have these equations:
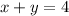 ( 1 )
( 1 )
y = -x^{2}+ 2x + 4 ( 2 )
Equation ( 2 ) can be rewritten as:
-y = x^{2} - 2x - 4;
And Equation ( 1 ) can be rewritten as:
x + y = 4; y = 4 - x, but also -y = x - 4;
So,
-y = x^{2} - 2x - 4, and
-y = x - 4;
That is, the logical formula previously described above.
Second Step: solving the system in the way proposed
If -y = x^{2} - 2x - 4, and
-y = x - 4; then,
x^{2} - 2x - 4 = x - 4 .
x^{2} - 2x - 4 -( x - 4 ) = 0 .
x^{2} - 2x - 4 -x + 4 ) = 0 .
x^{2} - 2x -x + 4 - 4 = 0, where ( 4 - 4 = 0 ), that is
x^{2} - 3x = 0;
x^{2} - 3x = 0, where x is a common factor, so
x * (x - 3) = 0.
For this product to be true,
x = 0 or
x - 3 = 0 ⇒ x = 3 .
Having these values for x (two values, x = 0 and x = 3), we can find the other values for y, that is:
We know that x + y = 4 (Equation 1), then
For x = 3;
3 + y = 4 , and
y = 4 - 3 = 1; y = 1 .
So, P1 = ( 3, 1 );
For x = 0;
0 + y = 4 or y = 4 .
So, P2 = ( 0, 4 ).
Proving these results
Using equations ( 1 ) and ( 2 ):
For P1 = ( 3, 1 ),
3 + 1 = 4 ( 1 )
1 = -(3)^{2} + 2*(3) + 4 ( 2 ) or
1 = -(9) + 6 + 4 = -9 + 10 or
1 = 1 .
For P2 = ( 0, 4 ),
0 + 4 = 4 ( 1 )
4 = -(0)^{2} + 2*(0) + 4 ( 2 ) or
4 = 0 + 0 + 4 = 4 or
4 = 4 .