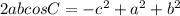Question

The law of cosines is a2+b2-2abcosc=c^2 find the value of 2abcosc

Answer 1

For this case we have the following equation:

`image`

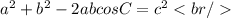
To find the value of 2abcosC we must follow the following steps:

Subtract a ^ 2 on both sides of the equation:

`image`

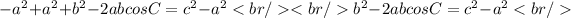
Subtract b ^ 2 on both sides of the equation:

`image`

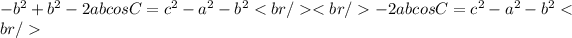
Multiply both sides of the equation by -1:

`image`

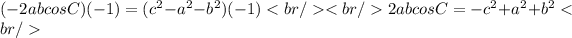
Answer:

the value of 2abcosC is:

`2abcosC = -c ^ 2 + a ^ 2 + b ^ 2`

Answer 2

The value of
`2ab\cos C` is
`a^2+b^2-c^2`

Explanation:

Given : The laws of cosine is
`a^2+b^2-2ab\cos C=c^2`

We have to find the value of
`2ab\cos C`

Consider the given formula for laws of cosine,

`a^2+b^2-2ab\cos C=c^2`

Subtract both side
`c^2`, we have,

`a^2+b^2-2ab\cos C-c^2=0`

Add
`2ab\cos C` both side, we have,

`a^2+b^2-c^2=2ab\cos C`

Thus, The value of
`2ab\cos C` is
`a^2+b^2-c^2`