Question

Given the system of equations, what is the x-coordinate of the solution? (matrix)

y = 3 -1/2 x
3x + 4y = 1

22
-17/2
-11

Answer 1

3x + 4(3-1/2x) = 1 Input Values of Y
3x + 12 - 2x = 1 Expand
(-12) x + 12 = 1 (-12)

Answer : C (x = -11)

Answer 2

-11

Explanation:

The given system of equations solved by matrix method is to arrange all coefficients into a matrix, and then making zeros in specific columns and rows, until we get an equation with just one variable.

`\left \{ {{y=3-(1)/(2)x } \atop {3x+4y=1}} \right.`

`\left \{ {{(1)/(2)x+ y=3} \atop {3x+4y=1}} \right.`

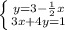
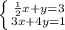
In matrix arrangement:

`\left[\begin{array}{ccc}(1)/(2) &1&3\\3&4&1\end{array}\right] \\`

Multiplying by 4 the first row and then subtracting with the second row, we have:

`\left[\begin{array}{ccc}-1 &0&11\\3&4&1\end{array}\right]`

From the firs row, we find that:

`-x+0y=11\\x=-11`

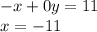
Therefore, the right answer is -11.