We need to find the derivative of a function, but if we look at the function is a quotient. Then we can use the rule for the derivative of a quotient:
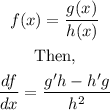
In this case, we have:
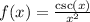
We can call:
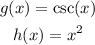
Now we apply the rule:
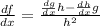
We know that the derivative of h(x) = x^2 is 2x, and the derivative of g(x) = csc(x) is [-cot(x)csc(x)]
Replacing the values:
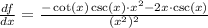
Simplifying:
We can factor out csc(x)*x in the numerator and solve the square in the denominator
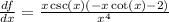
Finally, we can factor the (-1) inside the parentheses and cancel out the x in the numerator:
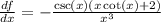
And this is the final answer.